INTERAKČNÍ TEORIE ŠKOLY
Pavel Kučera a Zbyšek Hlinka, © 1980
Je mnoho způsobů, jak si můžeme objasnit školní dění. Jedním z klasických je například vyprávění ze zkušeností, jak to udělal Jaroslav Žák v knize Študáci a kantoři aj. My jsme se pokusili o netradiční způsob výkladu - vysvětlení pomocí kvazičástic.
Kvazičástice (jakočástice) jsou kvanta zavedená k objasnění určitého problému. Kvazičástice tedy ve skutečnosti neexistují.
1. Základní interakce
Zavedeme si základní kvazičástici, která je příčinou veškerého školního dění. Je to koulon k (kapa). Koulon je kvantum známky 5.
DEFINICE: 1 koulon je připočtením 1 nejvyšší známky na konto žáka.
Dále budeme značit čárkou prekursory částic: např. k' je prokoulon.
Negovaná částice, tedy antičástice bude označována symbolem Ø předřazeným
před částici. Antikoulon tedy bude Øk.
Základní školní akcí je zkoušení.
DEFINICE: Zkoušení je proces takové doby trvání, aby dal vzniknout jednomu koulonu.
Předpokládejme, že impuls zkoušení je reprezentován hmotou, která se zúčastní látkové přeměny, která se musí udát, aby v kantorovi vznikl popud k vyzkoušení určitého nebožáka. Kvantováním této hmoty dostaneme kvazičástici zkoušion z. Interakcí těchto dvou částic dostáváme částici třetí, předměton P.
Zjednodušený vztah mezi těmito částicemi je
P + z ® k (1)
Vztah (1) je však velice nepřesný. Tento děj totiž vůbec samovolně neprobíhá.
Nyní si představme kantora ve všech možných situacích. Rozborem těchto stavů dostaneme, že kantor je nebezpečný toliko ve třídě. Tato situace je nebezpečnější pro studenty, kteří se již delší dobu nezúčastnili žádné interakce, neboť může vzniknout proces zkoušení. Zkoumejme tedy podrobněji situaci kantor ve třídě. Jestliže je ve třídě n potenciálních mučenců, pak pravděpodobnost vyzkoušení každého z nich je přímo úměrná době t, která od posledního zkoušení uběhla. Pravděpodobnost značíme A.
A ® 0, jestliže již zvoní a A ® ¥, jestliže je již vyřčeno nebožákovo jméno. Dále je A přímo měrné průměrnému počtu žáků vyzkoušených za jednu hodinu i, vzteku kantora V a zkoušecí proměnné R.
A =  (V + ti) (2)
n ³ i
(V + ti) (2)
n ³ i
Zkoušecí proměnná je závislá na mnoha faktorech a jejím odvozením se budeme zabývat
později. Pro hrubý výpočet ji můžeme zanedbat.
Kvantováním kantora ve třídě dostáváme kvazičástici kantoron kP, kde index P
značí příslušnost kantora, z něhož kantor vyšel, k určitému předmětu, jehož
kvantováním byla získána částice P.
Zavedením kantoronu do rovnice (1) dostáváme její přesnější znění:
P + kP + z ® k + kP
Přesto je to jen první přiblížení skutečnosti. Spějme však dále: určité interakce probíhají pouze v tzv. interakčních polích. Interakční pole vznikají interakcí a mají charakter fyzikálních polí.
Definujme si tedy koulovací pole M a zkoušecí pole E. Obě pole vznikají současně při interakci
P + kP + z ® k + kP
s pravděpodobností A. Jak je vidět, tato interakce proběhne poměrně zřídka proti interakci
P + kP ® z'
(kde z' je prozkoušion 1) která proběhne vždy. Proto je ten jistý žák zkoušen jen někdy.
Další veličinou, nutnou k objasnění vztahů ve škole, je smůlový faktor C. Je to velice složitá veličina, jejímž výpočtem se tady nehodláme zabývat. Je to určité množství štěstí či smůly, kterou zkoušený při akci má. Můžeme ji též chápat jako část pravděpodobnosti, s kterou koulon vznikne.
Další částicí, kterou si zavedeme, je studion s. Při učení dané látky se vynakládá určitá energie, jež se skokem mění na studion, je-li daný úkol naučen, popřípadě napsán. Vynaloží-li se energie jiným směrem nebo vynaloží-li se jí málo na daný úkol, vzniká samovolně potenciálně velmi nebezpečná kvazičástice antistudion Øs.
Nyní již můžeme zhruba sestavit rovnice, vyjadřující školní vztahy. Vždy proběhne interakce
P + kP ® z' (motivace)
a s pravděpodobností A probíhá interakce
P + KP ® E + M (aktivace)
Zkoušecího pole E je nutně třeba ke vzniku prozkoušionu 2.
E + z' ® z'' + kP (propagace)
Dále pak proběhnou v rychlém sledu další interakce.
z + z'' + Øs ® k' (terminace)
Prokoulon pak samovolně přechází za přítomnosti koulovacího pole M v koulon s pravděpodobností C.
M + k' ® k (katastrofa)
Pro úplnost je třeba ještě uvést opačné interakce, které dávají vznik antikoulonu:
z + z'' + s ® Øk'
M + Øk' ® Øk
s pravděpodobností C. Jak je vidět, vznik koulonu probíhá v 5 stupních: motivace, aktivace, propagace, terminace a katastrofa, přičemž žák může zasáhnout pouze do terminace a kantor pouze do aktivace. Katastrofu již nelze ničím odvrátit.
Je třeba ještě podotknout, že aktivace může probíhat místo
P + kP ® E + M,
která probíhá s pravděpodobností A, též interakcí
P + kP + kPMN ® E + M,
kde kPMN je kantoron kantora zasednutého na dotyčného nebožáka. kPMN je notným a účinným katalyzátorem této interakce. Tuto interakci může přerušit pouze jev, který se zove nekolegialita mezi kantory.
2. Vyšší interakce
(jen pro pokročilé)
Vznikem koulonu však dění ve škole nekončí, ale pokračuje vyššími interakcemi. Tyto interakce jsou odlišné od základních, neboť je nelze psát ve tvaru
x + y ® w
U vyšších interakcí se setkáváme s jevem, který se zove akumulace. Akumulace je zvyšování energetického stavu částic, přičemž se 2 částice spojí v l:
x + x ® x s vyšší energií.
Proto můžou akumulovat jen některé částice. Energetický stav částic se vyhodnocuje při akci účtování. Účtování (dříve konference) se značí | |. Účtování koulonů je tedy |k|. Při tomto procesu se hodnotí stav částic takto:
Je-li |x| větší nebo rovno kritické hodnotě Hx, pak částice x přechází v novou částici. Je-li |x| menší než kritická hodnota Hx, pak se energetický stav vrací na původní úroveň x.
Obecně: |x| ³ Hx Þ x ® y Ú |x| < Hx Þ x ® x
kde y je nová kvalita částice x.
Jak je vidět, problém bude pouze s výpočtem kritické meze Hx. První veličinou, kterou si zavedeme, bude zaujatost B kantora vůči nebožáku.
DEFINICE: Zaujatost B je množství sympatie či nesympatie vůči nebožáku takové, aby vznikla zaujatost.
Druhou veličinou je kapacita trpělivosti N.
DEFINICE: Kapacita trpělivosti se udává počtem nezodpovězených kantorových otázek žákem, než vznikne 1 koulon.
Zaujatost je také nepřímo úměrná chápavosti žáka e a despektu kantora vůči žáku a.
Despekt se střádá po velmi malých částech Da a je tedy součtem těchto hodnot:
a = 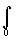 da
a =
da
a = 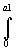 da = al
da = al
Kapacita trpělivosti je tedy
N = e - al
Dostáváme tedy zaujatost B jako součet všech minusových kapacit trpělivosti
B = 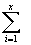 (ai - ei)
(ai - ei)
Sečteme-li zaujatost všech kantorů zúčastněných na konferenci, dostaneme hodnotu nevole
h = 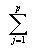 Bj
Bj
kde p je počet kantorů zúčastněných na konferenci.
Kritickou mez pak dostaneme vztahem
Hk = 5 - h
znaménko "-" je dáno tím, že čím více roste hodnota nevole, tím nižší je pak kritická hranice H.
čili Hk = 5 –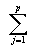
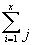 (ai - ei)
(ai - ei)
(5 je magické číslo)
Zavedeme si nyní novou kvazičástici napínon n.
|k| ³ Hk Þ k ® n
neboť:
je-li bilance koulonu vyšší než kritická koulonová mez, přechází koulon na napínon.
Napínony potom interagují na reparon r.
|n| ³ Hn Þ n ® r
Kritická napínonová mez je rovna součtu všech hodnot nevole, které kdy byly proti nebožákovi vedeny.
Hn = 5 – 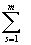
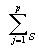
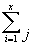 (ai - ei)
(ai - ei)
kde m je počet řízení, které kdy byly proti nebožáku vedeny.
Z napínonu vzniká reparon tedy mnohem snadněji než z koulonu napínon.
To je tedy vše, co bychom měli o vyšších interakcích vědět. Ještě je třeba podotknout, že těmto interakcím se někdy říká též silné nebo tvrdé.
3. Složené interakce
Složené interakce jsou rozšířením povídání o základních interakcích. Vznik napínonu nebo dokonce reparonu totiž zpětně ovlivňuje vznik koulonu: ovlivňování se děje ve dvou částech vzniku koulonu. V aktivaci
P + kP ® E + M
se pravděpodobnost A této interakce zvyšuje a tím tedy plyne pro žáka větší nebezpečí zkoušení. Dále se ovlivňování děje v katastrofě:
M + k' ® k
Tato interakce neprobíhá už s pravděpodobností C, ale s pravděpodobností CB. Podobně interakce
M + Øk' ® Øk
též neprobíhá s pravděpodobností C, ale s pravděpodobností 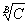 .
.
To znamená, že štěstí klesá, neboť úskoky kantora rostou a s nimi i těžkost otázky. Současně se ale zvyšuje zaujatost:
Bi = Bi - 1 + mp
kde Bi je nová zaujatost a Bi - 1 původní zaujatost. Jak je vidět, nebožák, když jednou do interakcí zabředne, těžko se dostává ven.
4. Interference
Mezi školní dění patří též velice významný jev - interference. Interference je komplexní jev, se kterým se setkáváme jak u základních, tak u vyšších interakcí. Je to působení jedné interakce na druhou. Klasickým příkladem interference je ovlivňování kantorů mezi sebou:
P1 + kΠ1 ® E + M /A
P1 + kΠ1 ® z'
E + z' ® z'' + kΠ1
z + z'' + Øs ® k'
k' ® k /C
¯
P2 + kΠ2 ® E + M /A
P2 + kΠ2 ® z'
E + z' ® z'' + kΠ2
z + z'' + Øs ® k'
k' ® k
↑
kΠ1
Z tohoto zdlouhavého zápisu je patrno několik skutečností:
a) interferenční ovlivňování značíme svislou šipkou
b) vznik koulonu při jednom předmětu ovlivní pravděpodobnost zkoušení při druhém předmětu a navíc pomluva žáka od prvního kantora zatvrdí více druhého kantora.
Další případ interference je působení inspektora na proces zkoušení. Je-li přítomen inspektor, pak je zkoušení situováno spíš na lepší žáky. Jakmile však inspektor přítomen není, propukne zkoušení opět v plné síle. Inspektor tedy není typickým inhibitorem (viz dále).
Jistě si vzpomínáte na zkoušecí proměnnou R z první kapitoly. Nadešel čas, abychom si o ní pověděli něco bližšího. Jak jsme již uvedli, je ovlivňována zaujatostí a hodnotou nevole, ale to není vše. Jistou úlohu hraje též inspektor a inhibitory. Je též ovlivňována okamžitými pohnutkami a stářím kantora (entropie).
Můžeme říci, že R roste se součinem všech špatných zpráv od ostatních kantorů P a se zaujatostí a nevolí,
tedy R = 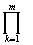 Pk +
Pk + 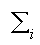 Bih = R =
Bih = R = 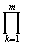 Pk + h2,
Pk + h2,
ale současně je ovlivňována přítomností inspektora.
Druh inspektora určuje proměnná inspektoron G Î <0; 1>. Je-li tedy 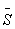 průměr známek dotyčného žáka, pak
průměr známek dotyčného žáka, pak
R = G (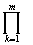 Pk + h2) :
Pk + h2) : 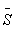
Vidíme, že lepší žáci jsou v přítomnosti inspektora v nevýhodě. R je však též nepřímo úměrné hodnotě inhibice I (viz dále): dostáváme tedy konečný tvar
R = 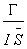 (
(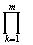 Pk + h2).
Pk + h2).
V případě, že inspektor není přítomen, inspektoron vypadá z rovnice a na jeho místo nastupuje
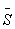 .
.
Existuje ještě mnoho druhů interferencí speciálních, ale ty již překračují rámec naší publikace.
5. Rezistence
Rezistence je odolnost vůči nějakému procesu. V našem případě jde o rezistenci vůči zkoušení. Rezistence lze nabýt různým způsobem:
a) vypěstovaná rezistence - žák si rezistenci vypěstuje sám,
b) vrozená rezistence - jméno nebo vzhled žáka nebo obojí inhibituje zkoušení,
c) existenční rezistence - zkoušení inhibitují jiné faktory, které žák nemůže ovlivnit.
V tomto pojednání se budeme zabývat pouze prvními dvěma případy (obzvláště 1. případem).
Inhibice je proces, při kterém se vyřazuje dočasně z činnosti nějaký komplex (tedy inhibice zkoušení je dočasná ochrana proti zkoušení).
Denaturace je proces, při kterém dochází k úplné destrukci komplexu nebo k jeho takovému poškození, že již není vůbec schopen vykonávat funkci komplexu určenou.
V celé této kapitole se tedy budeme zabývat výpočtem inhibiční hodnoty I. Jak je vidno, čím větší bude I, tím menší bude pravděpodobnost aktivace zkoušecího procesu.
a) Použijeme zvláštního typu vyšších interakcí - energetizační vyšší interakce. Jistě si vzpomenete na definici vyšších interakcí
|x| ³ Hx ® y
Energetizační reakce mají dva stupně:
|x| ³ Hx ® y hodnota střádané energie u y je Y. Je to reálné číslo a lze s ním počítat.
Schopnost takto interagovat mají antikoulony.
|Øk| ³ HØk ® Q
energetický stav je Q, čili teprve střádání Q má vliv na inhibici zkoušení.
Budeme se tedy opět zabývat výpočtem HØk. Je jasné, že bude tato hodnota přímo úměrná zaujatosti, a tedy i hodnoty nevole:
HØk = 5eh e je eulerovo číslo = 2,71…
Čili čím menší je hodnota nevole, tím menší je též HØk. Inhibiční faktor je tedy součtem všech energií Q:
I = 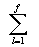 Q
Q
čili I = 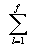 5elh
5elh
Tato rezistence je nejčastější. Je vidět, že nevzniká hned po první jedničce ze zkoušení (vznik Øk), ale teprve po neustálém vědění po dlouhou dobu.
b) I lze však dostat též jiným způsobem: pro kantora špatně vyslovitelným jménem nebo naopak hodně častým jménem. Ale tato rezistence nastává vůči získané rezistenci méně často a je krátkodobější (než si kantor na žákovo jméno zvykne). I je tedy přímo úměrné délce jména a počtu souhlásek a samohlásek v něm (souhlásky s, samohlásky a, délka slova d) a je nepřímo úměrné času t od seznámení kantora se žákem, tedy
I = 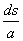 - t
- t
Může se vyskytnout šťastlivec, u kterého se vyskytnou oba případy:
I = (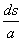 - t) +
- t) + 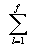 5elh
5elh
Vidíme, že v tomto případě když dozní rezistence vrozená, objeví se brzy rezistence vypěstovaná. Ještě je třeba připomenout, že rezistence vrozená odezní dříve než rezistence vypěstovaná, a že vypěstovaná rezistence přetrvává až do konce pololetí. Vrozené rezistence lze u určitého kantora použít jen jednou.
Tato teorie je spíš jen náčrtem obrovské a rozsáhlé teorie školy. V tomto kratičkém náčrtu jsou pouze naznačeny základní školní vztahy a přesný výpočet podle uvedených vzorečků není možný. Na to bychom potřebovali zvláštní testy na určování těžko měřitelných veličin, jako je např. vztek kantora. Tyto testy by však musel vytvořit psycholog. Tato teorie je tedy výchozím bodem pro teorii podrobnou, kterou bychom rádi vytvořili v budoucnu už s pomocí mnoha odborných odvětví.
Slovník
aktivace - povzbuzení k činnosti
akumulace - hromadění
denaturace - zbavování látek jejich přirozených vlastností
despekt - opovržení, pohrdáni
destrukce - rozklad
inhibice - zabránění
inhibitor - látka zpomalující nějakou reakci
interakce - vzájemné působení dvou nebo více činitelů
interference - vzájemné ovlivnění
katalyzátor - látka ovlivňující rychlost reakce, aniž do ní vstupuje
katastrofa - osudový obrat, neštěstí velkého rozsahu
komplex - soubor, celek
kvantování - dělení na kvanta
kvantum - množství, počet
kvazičástice - jakočástice
motivace - odůvodnění, zdůvodnění
potenciální - možný
prekurzorní - předběžný, nastalý před lhůtou
propagace - rozšiřování, rozmnožování
rezistence - aktivní odpor, odolnost vůči vnějším vlivům
terminace - ohraničení, omezení
Přehled částic
a - samohlásky
d - délka slova
e - eulerovo číslo
h - hodnota nevole
i – průměrný počet žáků vyzkoušených za hodinu
kP - kantoron
kPMN - kantoron kantora zasednutého na dotyčného žáka
m - počet řízení vedených proti žáku
p - počet kantorů na konferenci
r - reparon
s - souhlásky
t - čas
z - zkoušion
A - pravděpodobnost
B - zaujatost kantora vůči žáku
C - smůlový faktor
E - zkoušecí pole
Hx - kritická hodnota
I - inhibiční hodnota
M - koulovací pole
N - kapacita trpělivosti
P - počet kantorů
R - zkoušecí proměnná
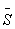 - průměr známek
- průměr známek
V - vztek kantora
a - despekt kantora vůči žáku
e - chápavost žáka
k - koulon
n - napínon
s - studion
G - inspektoron
Q - energetický stav
P - předměton
Ø - negace